1.13 Vegers linjeføring

Vegers linjeføring, dvs. i hovedsak horisontalkurver, stigninger og høy-/lavbrekk, kan på mange ulike måter påvirke ulykkesrisikoen.

Horisontalkurver har, hvis alt annet er likt, flere ulykker når de er krappe, når de har stor retningsendring, når de har for lite overhøyde (helning mot kurvens innside som tar opp sentrifugalkrefter og sørger for vannavrenning), når de har for korte overgangskurver (overgang mellom kurve og rettstrekning) og når de kommer «overraskende». Sistnevnte innebærer at kurver som f.eks. kommer etter en lengre rett strekning og krappe kurver som kommer etter flere slake kurver, har høyere risiko enn kurver som samsvarer bedre med vegens linjeføring for øvrig.

Stigninger og høy-/lavbrekk har langt mindre betydning for ulykkesrisikoen enn horisontalkurvatur, men både bratte og lange stigninger, samt krappe høy- og lavbrekk har i gjennomsnitt flere ulykker enn flate strekninger.

Også vegens geometriske konsistens påvirker ulykkesrisikoen. Med dette menes vegens linjeføring over en lengre strekning. Indikatorer for vegens geometrisk konsistens kan være definert på mange ulike måter, for eksempel antall krappe kurver, nødvendige fartsendringer eller samlede retningsendringer. Strekninger med uheldig linjeføring kan ha opptil dobbelt så høy ulykkesrisiko som strekninger med en «god» linjeføring, men resultatene spriker mye mellom studiene.

Problem og formål

Vegens linjeføring påvirker bl.a. fart, siktforhold og føreratferd, samt hvilke krefter som virker på kjøretøyet. Ulykkesrisikoen er som regel høyere i kurver enn på rette strekninger (Bíl et al., 2019; Milton & Mannering, 1996). Ulykkestyper som er overrepresentert i kurver, er bl.a. utforkjøringsulykker (Wang et al., 2017), fartsrelaterte ulykker og ulykker hvor føreren har vært beruset (Høye, 2020), samt ulykker hvor dårlig vegdekke eller vanskelige kjøreforhold har bidratt til ulykken (Yu et al., 2015).

Offisiell ulykkesstatistikk fra Norge (2018-2022) viser at 48 prosent av møte- og utforkjøringsulykkene skjedde i kurver. Utforkjøringsulykker er i gjennomsnitt mer alvorlige når de skjer i kurver enn på rette strekninger; av alle utforkjøringene som skjedde i kurver, var 21 prosent alvorlige ulykker (ulykker med drepte eller hardt skadde), mens 16 prosent av utforkjøringene på rette strekninger var alvorlige. I møteulykker er det ingen stor forskjell i skadegraden mellom kurver og rette strekninger; her er andelen alvorlige ulykker på 26 prosent i kurver og 28 prosent på rette strekninger.

Hvor mange ulykker som skjer i stigninger (oppover- eller nedoverbakker) eller på høy-/lavbrekk, fremgår ikke av offisiell ulykkesstatistikk.

En studie av fartsrelaterte dødsulykker i Norge i 2005-2015 (Høye, 2017) viser at ulykker i kurver langt oftere er relatert til høy fart enn andre ulykker. Figur 1.13.1 viser fordelingen av dødsulykkene i og utenfor kurver på tre ulike fartskategorier. Ulykker i kurver er også langt oftere relatert til rus; blant dødsulykkene i kurvene var 20 prosent relatert til rus, mens det blant de øvrige dødsulykkene kun var 10 prosent som var relatert til rus.

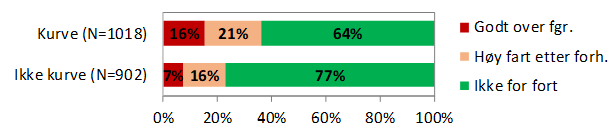
Figur 1.13.1: Fordeling av dødsulykkene i Norge (2005-2015) i og utenfor kurver på tre fartskategorier («Godt over fgr.»: fart over grense for førerkortbeslag; «Høy fart etter forh.»: for høy fart etter forholdene, ikke nødvendigvis over fartsgrensen og ikke over grensen for førerkortbeslag; «Ikke for fort»: Ingen av de to foregående kategoriene).

En studie av dødsulykker med motorsykkel i Norge (2005-2014) viser at 57 prosent av ulykkene skjedde i horisontalkurver, 23 prosent skjedd på stigninger (opp eller ned) og 14 prosent skjedde i høybrekk. Analysene som er gjort av Statens vegvesens ulykkesanalysegruppene, viser at spesifikke egenskaper ved horisontalkurver har bidratt til 15 prosent av ulykkene, dvs. til omtrent hver fjerde ulykke som skjedde i en kurve. Dermed er kurveforløpet den vegegenskapen som har bidratt til flest motorsykkelulykker. Spesifikke egenskaper ved kurvene som har bidratt til ulykker, er bl.a. krappe kurver, uoversiktlige kurver og sammensatte kurver med varierende radius. Egenskaper ved stigninger eller høybrekk har kun bidratt til svært få ulykker (2 prosent).

Formål med bedring av vegers linjeføring og siktforhold er å redusere ulykkesrisikoen og å forbedre framkommeligheten.

Beskrivelse av tiltaket

Med en vegs linjeføring menes horisontalkurver, vertikalkurver (høy-/lavbrekk) og stigninger. Konkrete egenskaper ved linjeføringen er beskrevet under Virkning på ulykker. Krav til vegens linjeføring på norske veger er beskrevet vegnormalen (Statens vegvesens håndbok N100, 2023). Grunnlaget for kravene er beskrevet i Statens vegvesens håndbok V120 (2022).

Virkning på ulykkene

Hvordan enkelte linjeføringselementer henger sammen med ulykkesrisiko er undersøkt i en omfattende litteraturstudie av Elvik (2023). Tabell 1.13.1 viser en oversikt over resultatene, og resultatene for de enkelte parameterne er beskrevet i avsnittene under.

Tabell 1.13.1: Betydningen av linjeføringselementer for antall ulykker. Relative ulykkestall.

Linjeføringselement	Referanse	Mindre gunstige verdi	Relativt ulykkestall
Horisontalkurveradius	600 m	50 m	3,58
Horisontalkurvers avbøyningsvinkel	30 grader	100 grader	2,52
Horisontalkurvers lengde	50 m	600 m	5,86
Overhøyde i horisontalkurver (#)	10 %	0 %	1,21
Variasjon i overhøyde i horisontalkurver (#)	0 %	10 %	1,21
Forekomst av overgangskurve (#)	Ja	Nei	1,12
Økning av lengde på overgangskurve (#)	10 m	0 m	1,02
Lengde av rett strekning før kurve	0,1 km	1,0 km	1,38
Radius i nabokurver	50 m	600 m	1,11
Antall kurver før en gitt kurve (#)	5	0	1,41
Stigning før horisontalkurve (#)	0 %	1 %	1,45
Fall før horisontalkurve (#)	0 %	1 %	1,56
Horisontalkurve i høybrekk	Nei	Ja	1,91
Horisontalkurve i lavbrekk	Nei	Ja	2,08
Stigningsgrad (absoluttverdi)	0 %	7 %	1,30
Stigningers lengde	0,1 km	1,0 km	8,72
Stoppsiktkrav ved høybrekkskurver	Oppfylt	For kort	1,23-1,34
Siktlengde generelt	227 m	45 m	1,58

(#) Resultatet bygger på én norsk undersøkelse

Horisontalkurver: Radius, avbøyningsvinkel og lengde

Horisontalkurver er som regel utformet som sirkelbuer. Mellom en rett strekning og sirkelbuedelen av en horisontalkurve er det som regel en overgangskurve (se nedenfor under Overgangskurver). Horisontalkurver kjennetegnes av radius, avbøyningsvinkel og retningsendring:

• Radius: Kurver med en liten radius er krappere enn kurver med stor radius
• Avbøyningsvinkel: Kurver med en stor avbøyningsvinkel har stor retningsendring
• Lengde: Ved samme avbøyningsvinkel er krappe kurver kortere enn slake kurver.

Sammenhenger mellom disse kurveegenskaper og ulykker som er funnet i studien til Elvik (2023), er beskrevet i følgende. Sammenhengene er også undersøkt i en norsk studie som er basert på ulykker i kuver på norske tofelts-landeveger (Elvik & Haugvik, 2023). I denne studien ble det funnet en større sammenheng mellom kurveradius, avbøyningsvinkel, kurvelengde og ulykker enn i oversiktsstudien til Elvik (2023).

Radius: Antall ulykker øker med synkende radius, dvs. at krappere kurver har flere ulykker enn slake kurver, hvis alt annet er likt. Sammenhengen mellom kurveradius og relativt antall ulykker er vist i figur 4.13.2.

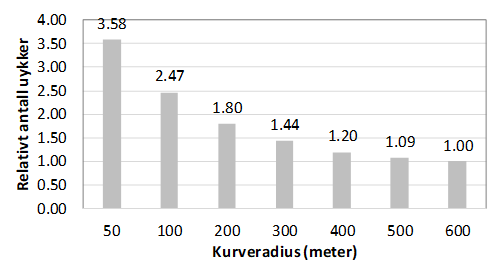
Figur 4.13.2: Sammenhengen mellom kurveradius og relativt antall ulykker (1 for kurver med en radius på 600 meter), basert på 47 empiriske studier (Elvik, 2023).

Sammenhengen mellom horisontalkurveradius og ulykker i tunnel er undersøkt av Høye et al. (2019) med hjelp av ulykkesmodeller som er basert på ulykker i norske vegtunneler (2008-2017). Resultatene viser at helt rette tunneler i gjennomsnitt har 69 prosent flere personskadeulykker enn tunneler som har minst én kurve med en radius på 600 meter eller mindre. Det er ingen vesentlige eller signifikante forskjeller mellom tunneler med kurver med ulik radius under 600 meter.

Avbøyningsvinkel: Elvik (2023) viser at sammenhengen mellom avbøyningsvinkel og antall ulykker er omtrent lineær og at kuver med en avbøyningsvinkel på 100 grader i gjennomsnitt har 2,52 ganger så mange ulykker som kurver med en avbøyningsvinkel på 30 grader. Dette er basert på 19 enkeltresultater. Tre av enkeltresultatene viser motsatt effekt, dvs. færre ulykker i kurver med større avbøyningsvinkel.

Kurvelengde: Lengre kurver har flere ulykker hvis alt annet er lik. Elvik (2023) viser at en økning av kurvelengden fra 50 til 600 meter (12-dobling av lengden) i gjennomsnitt fører til en økning av antall ulykker med en faktor på 5,86, når kurven har samme radius (kurven vil da ha større avbøyningsvinkel). Sammenhengen er tilnærmet lineær.

Kurveradius og fart: I kurver med liten radius er det ikke mulig å kjøre like fort som i kurver med større radius når overhøyden er den samme. Minste horisontalkurveradius er for eksempel 250 meter på hovedveger med fartsgrense 80 km/t og på 800 meter på veger med fartsgrense 110 km/t (N100, 2023).

Studier som har undersøkt sammenhengen mellom kurveradius og fart, viser at farten går ned med synkende kurveradius ved radius under 500 meter, mens farten er relativt uavhengig av kurveradius i kurver med radius over 500 m (Cvitanic et al., 2013). Dette er uavhengig av avbøyningsvinkelen (retningsendringen) i kurven. Ved mindre kurveradius går farten ned, og nedgangen er større jo krappere kurven er (Donnell et al., 2018; Schmidl, 2011).

Horisontalkurver: Overhøyde

Overhøyde er kjørebanens tverrfall i horisontalkurver, dvs. at kjørebanen har en helning til innsiden av kurven. Overhøyden tar, sammen med sidefriksjonen, opp sidekrefter ved kjøring i kurver; i kurver uten overhøyde hadde det derfor vært stor risiko for utforkjøringer. I tillegg bidrar overhøyden til vannavrenning. Ved for stor overhøyde øker imidlertid risikoen for at biler kan skli mot innsiden av kurven.

I Norge er det gitt faste verdier for overhøyden ved ulike kurveradier som ligger mellom 3 prosent for slake kurver og 8 prosent for krappe kurver (Statens vegvesen, V120, 2022). Det er også gitt kriterier for når kurver skal ha overhøyde; for eksempel ved fartsgrense 80 km/t skal kurver med en radius under 2500 meter ha overhøyde. Slakere kurver skal ikke ha overhøyde, men takfall, dvs. at vegbanen heller mot utsiden av kjørefeltene i begge retninger.

Elvik (2023) finner at kurver uten overhøyde i gjennomsnitt har 21 prosent flere ulykker enn kurver med en overhøyde på 10 prosent. Dette kan ikke generaliseres da nødvendig overhøyde avhenger av kurvens radius. Det er likevel rimelig å anta at kurver med for lite overhøyde har økt ulykkesrisiko.

Elvik (2023) viser videre at kurver hvor overhøyden varierer, i gjennomsnitt har 21 prosent flere ulykker enn kurver hvor overhøyden ikke varierer. Dette gjelder variasjon i overhøyden på sirkelbuedelen av kurven.

Horisontalkurver og friksjon

Hvilken fart det er mulig å kjøre i en kurve, avhenger i hovedsak av kurvens radius og overhøyde samt vegdekkets friksjon. Himes og Donnell (2020) har utviklet et mål på kurvers «pålitelighet» (reliability) som er basert på forholdet mellom nødvendig og faktisk friksjon. Resultatene viser at jo høyere friksjonen er i forhold til kurvens radius, overhøyde og fartsnivå, og jo mindre dette forholdet varierer, desto færre ulykker kan man forvente i kurven. Dette viser at man må ta hensyn til kombinasjonen av ulike forhold (radius, overhøyde, fart og friksjon) for å vurdere utforkjøringsrisikoen i en kurve, og at det ikke er tilstrekkelig å vurdere kun én faktor om gangen.

Horisontalkurver: Overgangskurver

Overgangskurver er den delen av vegen som ligger mellom en rett strekning og sirkelbuedelen av en horisontalkurve. Overgangskurver er normalt utformet som klotoider, dvs. at de har en varierende radius som endrer seg jevnt over hele klotoidelengden.

Elvik (2023) viser at kurver uten overgangskurve i gjennomsnitt har 12 prosent flere ulykker enn kurver uten overgangskurve. Studien viser videre at kurver med kortere overgangskurver har flere ulykker enn kurver med lengre overgangskurver. For hver 10 meter reduksjon i lengden på overgangskurven øker antall ulykker med 2 prosent. Resultatene lar seg ikke generalisere da behovet for og utforming av overgangskurver avhenger av andre kurveegenskaper som radius og krav til overhøyde (jf. Statens vegvesens hånd håndbok V120, 2022).

Horisontalkurver: Strekning før kurven

Risikoen i kurver avhenger ikke bare av kurveegenskapene, men også av hvordan strekningen før kurven er utformet, bl.a. av lengden på den rette strekningen før kurven, radius i nabokurver og antall kurver før den aktuelle kurven. Elvik (2023) viser at antall ulykker i kurver øker:

• Med økende lengde på den rette strekningen før kurven: Øker man lengden på den rette strekningen før kurven fra 100 meter til 1 kilometer, øker antall ulykker i kurver i gjennomsnitt med 38 prosent.
• Med økende radius i nabokurven: Øker denne fra 50 til 600 meter (dvs. har man en slak istedenfor en krapp kurve før den aktuelle kurven), øker antall ulykker i kurven med 11 prosent.
• Med synkende antall kurver før den aktuelle kurven: Er det ingen istedenfor fem kurver før den aktuelle kurven, øker antall ulykker i den aktuelle kurven med 41 prosent.

Alle sammenhengene er tilnærmet lineære. Sammenhengene kan forklares med at det er vanskeligere for bilførere å tilpasse farten i kurver når disse kommer «overraskende» og krever en stor fartsreduksjon, enn når kurven oppleves som konsistent med vegens linjeføring for øvrig.

I vegnormalen (N100, 2023) stilles for hver dimensjoneringsklasse krav til minste (for de krappeste kurven også største) radius på nabokurver. Det stilles ingen krav til rette strekninger eller antall kurver før horisontalkurver.

Horisontalkurver: Kombinasjoner med stigninger og vertikalkurvatur

Horisontalkurver med stigninger / fall før kurven: Elvik og Haugvik (2022) viser at både stigninger og fall før horisontalkurver øker antall ulykker i kurven.

• Fall før kurven: Antall ulykker i kurven øker med 56 prosent ved et fall på 1 prosent og med 51 prosent ved et fall på 7 prosent.
• Stigning før kurven: Antall ulykker i kurven øker med 45 prosent ved en stigning på 1 prosent og med 5 prosent ved en stigning på 7 prosent.

Horisontalkurver i høy- / lavbrekk: Elvik (2023) viser at krappe kurver medfører større ulykkesøkning når de ligger i høy- eller lavbrekk enn når de ligger på en flatt veg eller en veg med jevn stigning eller fall. I gjennomsnitt er antall ulykker i horisontalkurver 91 prosent høyere i høybrekk og 108 prosent høyere i lavbrekk enn på flatt veg eller en veg med jevn stigning/fall. Dette er basert på kun én amerikansk studie.

I praksis vil antall ulykker i kurver avhenge av vegens horisontale og vertikale linjeføring over en lengre strekning. Retningslinjer og eksempler er gitt i Statens vegvesens håndbok 120. Her vises for eksempel hvordan uheldige kombinasjoner av horisontal og vertikal linjeføring kan gi førere et misvisende inntrykk av vegens videre forløp.

Stigninger

Elvik (2023) viser at det i gjennomsnitt er flere ulykker i stigninger enn på en flat veg. Både formen på sammenhengen og relativ ulykkesrisiko på bratte stigninger er imidlertid usikre. Elvik (2023) viser at man kan komme fram til ulike konklusjoner, avhengig av den metodiske tilnærmingen:

• Sammenheng mellom stigning og antall ulykker er tilnærmet lineær; stigninger på 7 prosent har i gjennomsnitt 32 prosent flere ulykker enn en helt flatt veg (basert på medianverdier i de enkelte studiene).
• Økende stigningsgrad medfører flere ulykker, og ulykkesøkningen blir større jo brattere stigningen er; stigninger på 7 prosent har i gjennomsnitt omtrent dobbelt så mange ulykker som en helt flat veg (basert på gjennomsnittlige resultater fra de enkelte studiene).

Når det gjelder stigningens lengde er resultatene mer konsistente. Elvik (2023) viser at lengre stigninger har flere ulykker enn korte stigninger. Sammenhengen er tilnærmet lineær og en stigning på 1 km lengde har i gjennomsnitt 8,72 ganger så mange ulykker som en stigning på 100 meter lengde. Antall ulykker øker med andre ord mindre enn lengden på stigningen.

Sammenhengen mellom stigninger og ulykker i tunnel er undersøkt av Høye et al. (2019) med hjelp av ulykkesmodeller som er basert på ulykker i norske vegtunneler (2008-2017). Resultatene viser at stigninger har relativt liten betydning for ulykker i tunnel. Stigninger har derimot stor betydning for branner i tunnel. Det er især lange og bratte stigninger (over 7 prosent) som øker brannrisikoen.

Vertikalkurver: Høy- og lavbrekk

Med høybrekk menes bakketopp og med lavbrekk menes bunnen av en nedoverbakke.

Stigning/fall før og etter høy-/lavbrekk: Elvik (2023) viser at både høy- og lavbrekk har flere ulykker når vegen før og etter høy-/lavbrekket er brattere. Figur 1.13.3 viser sammenhengen mellom stigning/fall før og etter henholdsvis høy- og lavbrekk og antall ulykker. Dette er basert på kun én amerikansk studie. Resultatene viser at ulykkesøkningen er noe større for lavbrekk med bratte fall enn ved høybrekk med bratte stigninger.

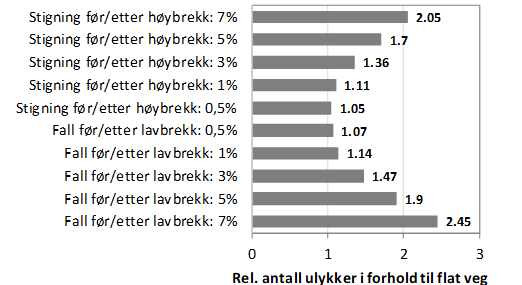
Figur 1.13.3: Sammenheng mellom stigning/fall før og etter henholdsvis høy- og lavbrekk og antall ulykker (Elvik, 2023).

Stoppsikt ved høybrekk: Elvik (2023) har basert på én studie funnet følgende virkninger på antall ulykker i høybrekk:

• Fjerne synlige sikthindre: -32 prosent
• Fjerne skjulte sikthindre: -38 prosent
• Krav til siktlengde oppfylt vs. ikke oppfylt: -19 til -24 prosent.

Siktlengder

I vegnormalen (Statens vegvesen, håndbok-N100, 2023; V120, 2022) er det fastsatt krav til stoppsiktlengden. Stoppsiktlengden avhenger av fart, stigningsgrad, reaksjonstid og friksjon (jf. Abdulhafedh, 2020). Håndbok V120 definerer minstekrav til stoppsiktlengden for hver dimensjoneringsklasse, både for rett veg og for kurver med ulike radier.

Ved vegutformingen påvirker kravene til stoppsiktlengden i hovedsak utforming av :

• Høybrekk: Jo lengre stoppsiktlengde som kreves, desto mindre krappe må høybrekk være
• Møte- og forbikjøringssiktlengder: Disse er direkte funksjoner av stoppsiktlengden
• Siktforhold i kurver, kryss og avkjørsler: Her må man sikre at sikten ikke blir hindret for eksempel av elementer i vegens sideterreng (jf. Mauga, 2016).

Elvik (2023) viser, basert på to eldre studier, at antall ulykker i gjennomsnitt er 58 prosent høyere på en veg hvor stoppsiktlengden er på 45 meter enn når stoppsiktlengden er på 227 meter. Dette kan ikke generaliseres da nødvendig stoppsiktlengde avhenger av en rekke ulike faktorer. Det er likevel rimelig å anta at (for) korte stoppsiktlengder medfører økt ulykkesrisiko.

Geometrisk konsistens

Geometrisk konsistens beskriver linjeføringen på lengre sammenhengende vegstrekninger. Forenklet sagt vil man som bilfører på en strekning med konsistent linjeføring ikke oppleve noen store overraskelser i form av uventede eller uventet krappe kurver. Sammenhengen mellom geometrisk konsistens og ulykker er undersøkt i en rekke empiriske studier som har delt inn veger i ulike linjeføringsklasser. Linjeføringsklassene er definert ut fra bl.a. andelen av strekningen som ligger i kurver, samlede retningsendringer, størrelsen på nødvendige fartsendringer og lignende.

Geometrisk konsistens antas å påvirke ulykkesrisikoen da bilførere tilpasser fart og forventningene ut fra vegegenskapene på hele strekningen. En krapp kurve vil dermed ikke komme overraskende på en strekning med mange krappe kurver. På en strekning som eller er nesten helt rett derimot, kan en krapp kurve komme uventet, slik at føreren ikke klarer å tilpasse farten like godt som når han hadde vært bedre forberedt.

Elvik (2023) har oppsummert resultater fra 21 slike studier. Figur 1.13.4 viser estimerte relative ulykkestall for vegstrekninger som her er delt inn i tre linjeføringsklasser, lav, middels og høy. I forhold til en veg med høy linjeføringsklasse, øker antall ulykker i gjennomsnitt med 20 prosent på en veg med middels linjeføringsklasse og med 39 prosent på en veg med lav linjeføringsklasse. Det er imidlertid stor variasjon mellom de enkelte studiene. For veger med lav linjeføringsklasse er laveste og høyeste anslag på relativt antall ulykker henholdsvis 1,02 og 2,04.

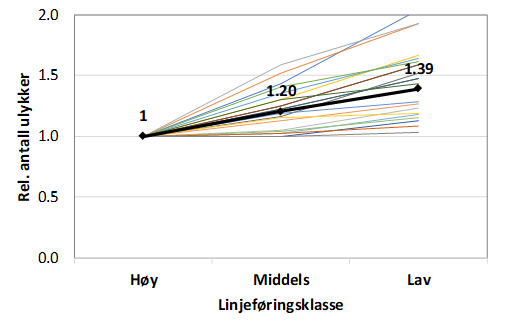
Figur 1.13.4: Relative ulykkestall på strekninger i ulike linjeføringsklasser som er funnet i 21 empiriske studier; tykk svarte linje viser gjennomsnittlige verdier.

Virkninger på fremkommeligheten

Vegers linjeføring påvirker trafikkens gjennomsnittsfart og fartsprofilet til det enkelte kjøretøy på ulike måter:

• Førere må tilpasse farten for å unngå utforkjøring; farten er derfor lavere i krappe kurver enn i slakere kurver.
• I stigninger er farten som regel høyere i nedoverbakker og lavere i oppoverbakker. Vaa (1991), viste at gjennomsnittsfarten i oppover­bakker med en stigning på 4 prosent er 7-8 km/t lavere enn på flat veg (70-72 km/t mot 78-79 km/t). I nedoverbakker på 4 prosent var gjen­nomsnittsfarten ca. 1-4 km/t høyere enn på flat veg (76-77 km/t mot 73-76 km/t).
• Både horisontal og vertikal linjeføring påvirker siktforholdene og dermed muligheten for forbikjøringer (Brenac, 1996)

Virkningen på det enkelte kjøretøys fart er større for tunge kjøretøy enn for lette (Skarra og Gabestad 1983). På tofeltsveger uten forbikjøringsfelt fører redusert fart for tunge kjøretøy også til reduser fart for lettere kjøretøy som kunne kjøre fortere, men som ikke kan kjøre forbi.

Virkninger på miljøforhold

Tiltak som påvirker fartsnivået, kan påvirke både støy og avgassutslipp, i den grad disse avhenger av fartsnivået. Økt fart kan føre til både økt støy og økte utslipp av enkelte typer avgasser. På den andre siden kan utbedring av linjeføringen redusere fartsvariasjon, noe som vil redusere drivstofforbruket og utslipp.

Veger med stiv linjeføring (store kurveradier som tillater et høyt fartsnivå) må oftere enn andre veger bygges på fyllinger eller i skjæringer og kan dermed utgjøre større naturinngrep enn veger med en linjeføring som er mer tilpasset til terrengets form.

Kostnader

Kostnadene til utbedring av vegers linjeføring varierer sterkt, avhengig av hvilken form for utbedring det er snakk om, hvor omfattende utbedringen er, terreng­forholdene på stedet og bebyggelsesgraden. Det er teknisk sett vanskeligere og dyrere å endre vegers linjeføring i byer og tettsteder enn i spredtbygd strøk. Veger som anlegges i fjell er dyrere enn ellers like veger i jordterreng. Når krav til linjeføring påvirker trasevalget for nye veger, kan dette potensielt ha stor effekt på anleggskostnadene.

Nytte-kostnadsvurderinger

Forholdet mellom nytte og kostnader ved utbedring av vegens linjeføring vil avhenge av mange ulike faktorer og det er derfor ikke mulig å oppgi generaliserbare nytte-kostandsbrøk.

Formelt ansvar og saksgang

Formelle krav og saksgang

Krav til nye vegers linjeføring og siktforhold er fastsatt i Statens vegvesens håndbok N100 Veg- og gateutforming (2023) og V120 Premisser for geometrisk utforming av veger (2022).

Linjeføringen fastlegges ved valg av dimensjoneringsklasse. I hver dimensjoneringsklasse er kravene til linjeføring tilpasset vegens forventede trafikkmengde og fartsgrense. Mange eksisterende veger har ikke linjeføring etter vegnormalstandard.

Ansvar for gjennomføring av tiltaket

Vegmyndigheten er ansvarlig for gjennomføring av utbedring av vegers linje­føring og dekker kostnadene ved slike tiltak. Dette innebærer at staten bærer kostnader til tiltak på riksveg, fylkeskommunen bærer kostnader til tiltak på fylkesveg og kommunen bærer kostnader til tiltak på kommunal veg.

Ifølge vegloven kan vegholderen pålegge grunneier å fjerne sikthindrende vegetasjon og andre sikthindre innenfor byggegrensene langs offentlig veg. Dersom pålegget ikke etterkommes, kan vegholder sørge for at arbeidet likevel blir gjort. Grunneieren skal da ha erstatning etter skjønn for ulemper og skader. Kostnader til siktrydding dekkes som vegutgifter.

Referanser

Abdulhafedh, A- (2020). Highway Stopping Sight Distance, Decision Sight Distance, and Passing Sight Distance Based on AASHTO Models. Open Access Library Journal, 7, 3. https://www.scirp.org/journal/paperinformation.aspx?paperid=99028

Bíl, M., Andrášik, R., & Sedoník, J. (2019). Which curves are dangerous? A network-wide analysis of traffic crash and infrastructure data. Transportation Research Part A: Policy and Practice, 120, 252-260.

Cvitanić, D., Vukoje, B., & Breški, D. (2012). Methods for ensuring consistency of horizontal alignment elements. Građevinar, 64(05.), 385-393.

de Oña, J., Garach, L., Calvo, F., & García-Muñoz, T. (2014). Relationship between predicted speed reduction on horizontal curves and safety on two-lane rural roads in Spain. Journal of transportation engineering, 140(3), 04013015.

Donnell, E. T., Kersavage, K., & Tierney, L. F. (2018). Self-Enforcing Roadways: A Guidance Report (No. FHWA-HRT-17-098). United States. Federal Highway Administration.

Elvik, R. & Haugvik, E. S. (2023). Safety of horizontal curves on rural two-lane roads in Norway. Traffic Safety Research, 5, 000026.

Fitzpatrick, K., Elefteriadou, L., Harwood, D.W., Collins, J.M., McFadden, J., Anderson, I. B., Krammes. R.A., Irizarry, N., Parma, K.D., Bauer, K.M. and Passetti, K. (2000). Speed prediction for two-lane rural highways. Report FHWA-RD-99-171.

Himes, S., & Donnell, E. (2020). Safety effects of horizontal curve reliability index. Transportation research record, 2674(9), 627-636.

Høye, A.K., Nævestad, T.O., & Ævarsson, G. (2019). Utvikling av modell for predikering av branner ulykker og havarier i vegtunneler. TØI-Rapport 1705/2019.

Høye, A.K., Vaa, T., & Hesjevoll, I.S: (2016). Temaanalyse av dødsulykker på motorsykkel 2005-2014. TØI-Rapport 1510/2016.

Høye, A.K. 82017). Dybdestudier av fartsrelaterte ulykker ved bruk av UAG-data. TØI-Rapport 1569/2017.

Høye, A. (2020). Speeding and impaired driving in fatal crashes—Results from in-depth investigations. Traffic injury prevention, 21(7), 425-430.

Mauga, T. (2016). Minimum Clearance Offsets for Providing Desired Stopping Sight Distances at Simple Curves with Variable Operating Speeds. Journal of Transportation Technologies, 6, 3. https://www.scirp.org/journal/paperinformation.aspx?paperid=65526

Schmidl, S. (2011). Untersuchung des Fahrverhaltens in unterschiedlichen Kurvenradien bei trockener Fahrbahn. Universität für Bodenkultur Wien, Institut für Verkehrswesen.

Wang, B., Hallmark, S., Savolainen, P., & Dong, J. (2017). Crashes and near-crashes on horizontal curves along rural two-lane highways: Analysis of naturalistic driving data. Journal of safety research, 63, 163-169.

Yu, R., Xiong, Y., & Abdel-Aty, M. (2015). A correlated random parameter approach to investigate the effects of weather conditions on crash risk for a mountainous freeway. Transportation research part C: emerging technologies, 50, 68-77.